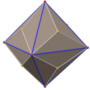
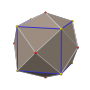
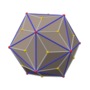
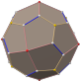
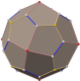
Pentakis dodecahedron

Pentakis dodecahedron
(Click here for rotating model)
Type	Catalan solid
Coxeter diagram
Conway notation	kD
Face type	V5.6.6 isosceles triangle
Faces	60
Edges	90
Vertices	32
Vertices by type	20{6}+12{5}
Symmetry group	Ih, H3, [5,3], (*532)
Rotation group	I, [5,3]+, (532)
Dihedral angle	156°43′07″ arccos(−80 + 9√5/109)
Properties	convex, face-transitive
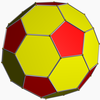Truncated icosahedron (dual polyhedron)	Net

3D model of a pentakis dodecahedron

In geometry, a pentakis dodecahedron or kisdodecahedron is a polyhedron created by attaching a pentagonal pyramid to each face of a regular dodecahedron; that is, it is the Kleetope of the dodecahedron. Specifically, the term typically refers to a particular Catalan solid, namely the dual of a truncated icosahedron.

Cartesian coordinates

Let $\phi$ be the golden ratio. The 12 points given by $(0,\pm 1,\pm \phi )$ and cyclic permutations of these coordinates are the vertices of a regular icosahedron. Its dual regular dodecahedron, whose edges intersect those of the icosahedron at right angles, has as vertices the points $(\pm 1,\pm 1,\pm 1)$ together with the points $(\pm \phi ,\pm 1/\phi ,0)$ and cyclic permutations of these coordinates. Multiplying all coordinates of the icosahedron by a factor of $(3\phi +12)/19\approx 0.887\,057\,998\,22$ gives a slightly smaller icosahedron. The 12 vertices of this icosahedron, together with the vertices of the dodecahedron, are the vertices of a pentakis dodecahedron centered at the origin. The length of its long edges equals $2/\phi$. Its faces are acute isosceles triangles with one angle of $\arccos((-8+9\phi )/18)\approx 68.618\,720\,931\,19^{\circ }$ and two of $\arccos((5-\phi )/6)\approx 55.690\,639\,534\,41^{\circ }$. The length ratio between the long and short edges of these triangles equals $(5-\phi )/3\approx 1.127\,322\,003\,75$.

Chemistry

The pentakis dodecahedron in a model of buckminsterfullerene: each (spherical) surface segment represents a carbon atom, and if all are replaced with planar faces, a pentakis dodecahedron is produced. Equivalently, a truncated icosahedron is a model of buckminsterfullerene, with each vertex representing a carbon atom.

Biology

The pentakis dodecahedron is also a model of some icosahedrally symmetric viruses, such as Adeno-associated virus. These have 60 symmetry related capsid proteins, which combine to make the 60 symmetrical faces of a pentakis dodecahedron.

Orthogonal projections

The pentakis dodecahedron has three symmetry positions, two on vertices, and one on a midedge:

Orthogonal projections

Projective symmetry	[2]	[6]	[10]
Image
Dual image

Concave pentakis dodecahedron

A concave pentakis dodecahedron replaces the pentagonal faces of a dodecahedron with inverted pyramids.

Convex (left) and concave (right) pentakis dodecahedron Related polyhedra The faces of a regular dodecahedron may be replaced (or augmented with) any regular pentagonal pyramid to produce what is in general referred to as an elevated dodecahedron. For example, if pentagonal pyramids with equilateral triangles are used, the result is a non-convex deltahedron. Any such elevated dodecahedron has the same combinatorial structure as a pentakis dodecahedron, i.e., the same Schlegel diagram. Spherical pentakis dodecahedron Family of uniform icosahedral polyhedra Symmetry: [5,3], (*532) [5,3]+, (532) {5,3} t{5,3} r{5,3} t{3,5} {3,5} rr{5,3} tr{5,3} sr{5,3} Duals to uniform polyhedra V5.5.5 V3.10.10 V3.5.3.5 V5.6.6 V3.3.3.3.3 V3.4.5.4 V4.6.10 V3.3.3.3.5 *n32 symmetry mutation of truncated tilings: n.6.6 Sym. *n42 [n,3] Spherical Euclid. Compact Parac. Noncompact hyperbolic *232 [2,3] *332 [3,3] *432 [4,3] *532 [5,3] *632 [6,3] *732 [7,3] *832 [8,3]... *∞32 [∞,3] [12i,3] [9i,3] [6i,3] Truncated figures Config. 2.6.6 3.6.6 4.6.6 5.6.6 6.6.6 7.6.6 8.6.6 ∞.6.6 12i.6.6 9i.6.6 6i.6.6 n-kis figures Config. V2.6.6 V3.6.6 V4.6.6 V5.6.6 V6.6.6 V7.6.6 V8.6.6 V∞.6.6 V12i.6.6 V9i.6.6 V6i.6.6 See also Excavated dodecahedron Cultural references The Spaceship Earth structure at Walt Disney World's Epcot is a derivative of a pentakis dodecahedron. The model for a campus arts workshop designed by Jeffrey Lindsay was actually a hemispherical pentakis dodecahedron https://books.google.com/books?id=JD8EAAAAMBAJ&dq=jeffrey+lindsay&pg=PA92 The shape of the "Crystal Dome" used in the popular TV game show The Crystal Maze was based on a pentakis dodecahedron. In Doctor Atomic, the shape of the first atomic bomb detonated in New Mexico was a pentakis dodecahedron.[1] In De Blob 2 in the Prison Zoo, domes are made up of parts of a Pentakis Dodecahedron. These Domes also appear whenever the player transforms on a dome in the Hypno Ray level. Some Geodomes in which people play on are Pentakis Dodecahedra, or at least elevated dodecahedra. References Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9) Sellars, Peter (2005). "Doctor Atomic Libretto". Boosey & Hawkes. We surround the plutonium core from thirty two points spaced equally around its surface, the thirty-two points are the centers of the twenty triangular faces of an icosahedron interwoven with the twelve pentagonal faces of a dodecahedron. Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 978-0-521-54325-5. MR 0730208. (The thirteen semiregular convex polyhedra and their duals, Page 18, Pentakisdodecahedron) The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN 978-1-56881-220-5 [2] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 284, Pentakis dodecahedron ) External links Weisstein, Eric W., "Pentakis dodecahedron" ("Catalan solid") at MathWorld. Pentakis Dodecahedron – Interactive Polyhedron Model Visual Polyhedra pentakis dodecahedron